论文名称:Learning Diverse and Discriminative Representations via the Principle of Maximal Coding Rate Reduction
地址:https://arxiv.org/abs/2006.08558
论文全文:https://arxiv.org/pdf/2006.08558
顶会收录:NeurIPS 2020

背景与动机
在深度学习中,如何从高维数据中学习低维结构,同时保持类别区分性,是一个重要的问题。现有的方法,如交叉熵损失(Cross-Entropy)、信息瓶颈(Information Bottleneck)和对比学习(Contrastive Learning)等,虽然有效但各有局限。本文提出 最大化编码率降低原则(Maximal Coding Rate Reduction,MCR²),作为一种信息论度量,最大化整个数据集与各类别子集之间的编码率差值,以学习多样且具区分性的表示。
核心理论
最大编码率降低原则(MCR²)
该原则旨在优化数据表示,使不同类别的特征相互正交(uncorrelated),而同一类别的特征尽可能压缩到低维子空间。
目标是 最大化整体数据的编码率 R(Z) 并最小化各类别的编码率 Rc(Z|Π),即: ΔR(Z,Π,ε)=R(Z,ε)−Rc(Z,ε∣Π)\Delta R(Z, Π, ε) = R(Z, ε) - Rc(Z, ε | Π)
其中,编码率 R(Z,ε)R(Z, ε) 通过数据协方差矩阵的行列式计算,度量数据的紧凑性。
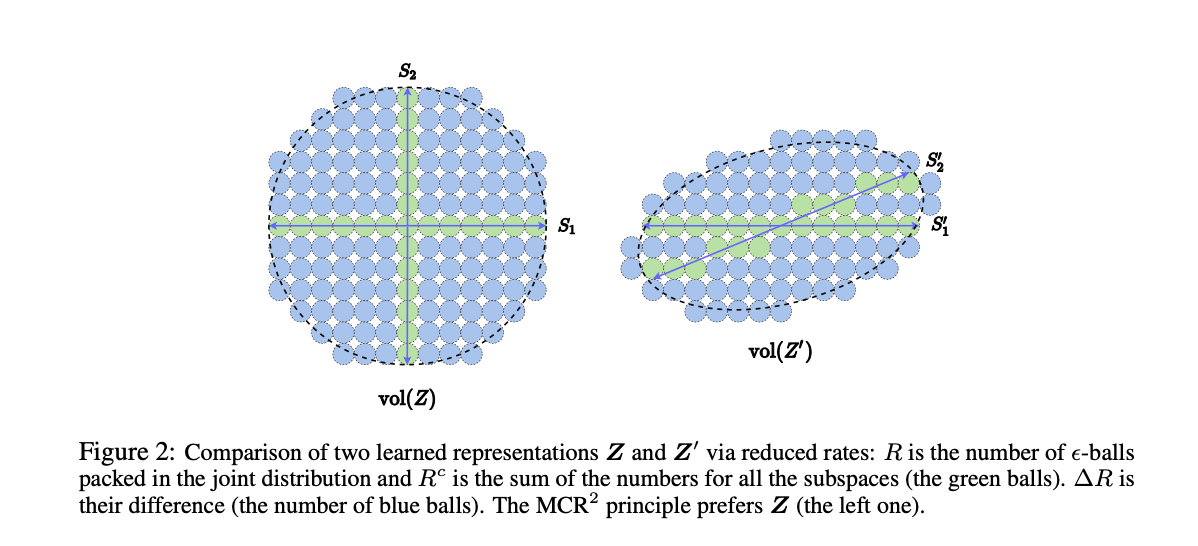
MCR²与现有方法的关系
交叉熵(CE):关注最终分类结果,但难以保证特征的结构化与可解释性。
信息瓶颈(IB):最大化特征与标签之间的互信息,同时最小化特征与输入数据之间的互信息,但可能牺牲泛化性和稳健性。
对比学习(Contrastive Learning):鼓励正样本靠近、负样本远离,但其优化目标较局限于样本对,而MCR²能优化整个数据集的结构。
理论分析
证明在 高维空间维度足够大、编码精度足够高 的情况下,MCR² 具有以下特性:
类别间区分性(Between-Class Discriminative):不同类别的特征正交。
类别内紧凑性(Within-Class Compressible):同类样本的特征落在低维子空间。
最大多样性(Maximally Diverse Representation):每个类别的特征维度尽可能高,但仍保持正交。
实验验证
监督学习(Supervised Learning)
采用 CIFAR-10 数据集,在 ResNet-18 上训练,使用 MCR² 替代交叉熵损失。
结果表明:
MCR² 学习到的特征更加正交,类别内的特征维度更高,相比交叉熵更鲁棒。
在标签噪声比例增加的情况下,MCR² 仍然保持较高的分类准确率,显示出更强的抗噪能力。
自监督学习(Self-Supervised Learning)
采用数据增强策略(如旋转、翻转等)模拟类别,通过最大化 MCR² 学习不变特征。
结果表明:
仅通过 MCR² 进行训练,无需额外的监督信息,即可获得良好的聚类效果。
采用子空间聚类算法 EnSC 进行分类,MCR² 取得了 比其他高度工程化方法更优的聚类性能。
对比实验
在不同数据集(CIFAR-10、CIFAR-100、STL-10)上,MCR² 均超越多种现有方法,如 JULE、DEC、DAC、DCCM 等。
通过 动态控制特征扩展与压缩(MCR²-CTRL),进一步优化无监督学习的训练效果,使学习到的特征更加稳定。
结论与未来工作
MCR² 统一了监督、自监督、无监督学习,提供了一种基于信息论的表示学习框架。
在监督学习中,MCR² 学习到的特征更具可解释性,并显著提升了模型的鲁棒性。
在自监督学习中,MCR² 仅凭数据增强即可学习高质量的特征,有望提升无标签数据的学习能力。
未来研究方向
进一步优化 MCR² 在深度网络中的层级应用,使不同层次的特征均能最大化编码率降低。
探索 MCR² 在其它任务中的应用,如生成模型、强化学习等。
研究 MCR² 在理论上的扩展性,例如如何更严格地界定优化目标的全局最优性。
总结:MCR² 提供了一种新的信息论视角,使得深度学习模型能够学习到更加多样化、稳健且具区分性的特征,在监督与自监督任务上均展现出优异性能,并在多个实验中超越现有方法。